Ranking athletes across weight classes

Point system from the statistical analysis of the King of Calisthenics competition

Overall, who is the strongest?

In this post, we wonder how to compare performances of athletes across weight classes.

We consider participants to the season 1 of the King of Weighted Calisthenics competition, an international and internet based event organized by Micha Schulz.
During this weighted calisthenics competition,

each participant had to get their weighted equipment and record their 1RMOne-repetition maximum: https://en.wikipedia.org/wiki/One-repetition_maximum attempts for dips, pull-ups and squats according to some specified rules (especially regarding the range of motion).

Using the work done by the International Powerlifting Association, we compute a formula similar to their IPF GL that allows to rank all participating athletes according to a point system.

The total mass lifted by a participant is the sum of all its three lifts,

\[\text{total lifted mass} = \text{dip} + \text{squat} + \text{pull-up},\]

and it mainly increases with the weight class, i.e., the heavier the athletes, the heavier they can lift.I would need a study/meta-analysis to back-up this claim. If you know a reliable one, please contact me and I will add a reference. Therefore, the total lifted mass is not a good scoring system to compare performances of athletes with different body features as it favors heavier athletes without considering the exerted effort relative to body features. If the total strength of heavier athletes is systematically larger than the one of heavier athletes, then this say something about the physiology of human beings (as a group) but not about the exerted effort of individual athletes.

On the other hand, the relative total lifted mass,

\[\text{relative total lifted mass} = \frac{\text{dip} + \text{squat} + \text{pull-up}}{\text{bodyweight}},\]

is said to systematically favor lighter athletesI would need a study/meta-analysis to back-up this claim. If you know a reliable one, please contact me and I will add a reference. and therefore is not a good scoring system. If the relative strength of lighter athletes is systematically larger than the one of heavier athletes, then this say something about the physiology of human beings (as a group) but not about the exerted effort of individual athletes.

So, how do we compute a (as good as possible) point system?

Computing a point system

We use an approach that we deem similar to the IPF one. The number of points of an athlete will be of the form

\[\text{points} = \frac{\text{total mass lifted}}{\text{predicted best lift} (\text{body features})},\]

where predicted best lift is a function that, given an athlete’s body features, compute its expected best lift. This function should therefore be related to the maximal strength performance an athlete can produce, given its body features. The number of points is then the ratio between its actual lift and this prediction. If this ratio is smaller than one, the athletes underperformed compared to the prediction, while a ratio larger than one should indicate a strong athlete that outperform this prediction. If the quality of the prediction is good enough, then this point system is reasonable enough.

However, the question of the prediction function remains. We first try to answer the following question: given an athlete’s body features, what is the largest reasonable total mass the athlete could have lift?

Computing a strength prediction function

Which body features?

The more body features we decide to use, the more complicated the formula might end up. We want to find measurable body features with a high predictive power for the performances of the best athletes with those features. A very simple hypothesis that is made by the IPF is that the best an athlete could have lift is a function of its bodyweight only. I will use this hypothesis in the remaining of this post. However, I do think that the height of an athlete is an important feature as well, as it is related to the length of most of the limbs. On the other hand, for high level powerlifting competition, such as the one organized by the IPF, athletes of similar height tends to have a similar physical build as opposed to what can be observed in the general population. In theory, one could try use the body composition measured and computed by a DEXA scan.https://en.wikipedia.org/wiki/Body_composition#DEXA However, finding a good formula is hard enough with the bodyweight only, and adding all those features won’t really simplify the task. One way around that would be to use neural network,https://en.wikipedia.org/wiki/Artificial_neural_network but this is a topic for another post!

Remark: Unfortunately, while it is quite an important body feature on its own, one could only compute a formula for male participants. There were not enough female participants at the king of weighted competition to compute any relevant formula. The reasoning is independent of the sex, but the specific computed number later are expected to be different depending on the sex.

We therefore aim to find a function predicted best lift such that,

\[\text{largest reasonable total lifted mass} = \text{predicted best lift} (\text{bodyweight}) .\]

Which function?

How do we find such a function?

Our model state that the strength of athletes increases with the bodyweight, hence the predicted best lift function should be strictly monotonic increasing.https://en.wiktionary.org/wiki/monotonic_increasing Our model also state that the strength of athletes obeys a law of diminishing return,https://en.wikipedia.org/wiki/Diminishing_returns i.e., the relative strength decreases, hence the predicted best lift function should be concave.https://en.wikipedia.org/wiki/Concave_function While we decided upon some necessary properties of our model, those are far from sufficient to pick a function. As far as I wanted to derive a formula based on necessary and sufficient propertiesIf you are a sport scientist interested in this topic and want to try a few ideas, please reach me out!, I am not a sport scientist and I will have to rely on existing formulas.

The IPF suggest the following function,

\[a - b \exp ( -c \times \text{bodyweight}),\]

where $a$, $b$, and $c$ are positive coefficients, and $\exp$ is the exponential function.https://en.wikipedia.org/wiki/Exponential_function As far as I am concerned, my first guess would have been to try something like

\[a + b \times \text{bodyweight} + c \ln (\text{bodyweight} + d),\]

where $a$, $b$, $c$ and $d$ are coefficients, and $\ln$ is the logarithm function.https://en.wikipedia.org/wiki/Natural_logarithm However, I am not a sport scientist so we will use the formula suggested by the IPF.

Which coefficients?

To find the coefficients $a$, $b$, and $c$ of the proposed formula, we will rely on the data from the king of weighted competition. The aim of the formula is to compute a reasonable best performance. Therefore, we first compute the considered top-20% athletes and then use those performances to compute the values of the coefficients.

By only using the subset of athletes that are top-performer, we ensure that our function will effectively compute an approximation of the expected best lift of an athlete given its bodyweight. The threshold must be high enough so that we only consider top-performer. However, it should be low enough that we have enough data, represents of almost all bodyweight and that we consider more than the absolute best. Considering only the absolute best would be a mistake as it could diminish the number of points a participants of similar weight would receive because a once-in-a-century athletes has similar features. Hence, the expression reasonable best lift that we used.

To compute the coefficients, we use a technique called regression analysis,https://en.wikipedia.org/wiki/Regression_analysis where we try to find the coefficients that fit the data the best. Let’s do that and see how it looks!

In the following graph, the color of the points is related to the number of points: the bluer, the smaller the number of points, the redder, the higher the number of points. The size and transparency of the points are also related to the number of points: the bigger and darker, the larger the number of points.

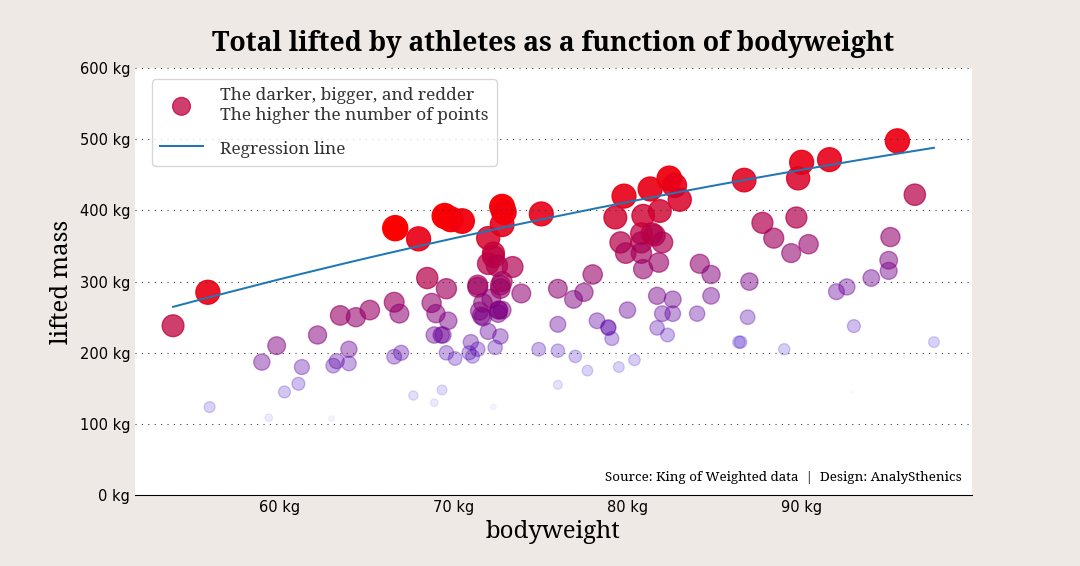
The plotted curve does seem like the graph of a descent largest reasonable total lifted mass function. The attributed number of points also does seem to be coherent with the point system we wished to build.

Overall winner of the competition

No need to prolong the suspense any longer, according to this point system, the overall winner of the competition is Joel Catena!

Congratulations!

With that, we will close this post. Thank you very much for reading up to this point! If you have any remark or question, feel free to reach me, my door is always open!